Ebben a tananyagrészben az első példaprogramjainkban leggyakrabban használt alaptípusú változók jellemzőiről, és ehhez a témához kapcsolódó tudnivalókról lesz szó.
Az itt leírtakat természetesen nem kell bemagolni, viszont egyrészt érdemes egyszer átolvasni, hogy tisztában legyünk vele, hogy ilyen jellegű hibák is előfordulhatnak a programjainkban, másrészt pedig ha a későbbiek során esetleg szükségünk lenne valamilyen témához kapcsolódó információra, kódrészletre, akkor ez a tananyagrész talán segíthet.
Előző tananyagrész: gyakori műveletek
Következő tananyagrész: alapvető típuskonverziók
Tartalom
- alaptípusok és alaptípusú változók
- típusminősítők (const, volatile)
- típusmódosítók (short, long, longlong, unsigned)
- típusmódosítók a literálokban
- legkisebb és legnagyobb értékek (pl. std::numeric_limits<int>::min())
- egyéb információk (pl. std::numeric_limits<double>::digits10())
- méret lekérdezése (sizeof)
- méret típusa (size_t)
- alaptípusok mérete a C++ szabvány szerint
- fix méretű int típusú változók (pl. int32_t)
- hogyan válasszunk a különböző típusok közül:
short int, int, long int, long long int
float, double, long double
int vs double
int, double vs string - az egyes típusokról bővebben:
char típus (ascii tábla, signed/unsigned char, escape karakter, szóköz, tabulátor bekérése)
int típusok (túlcsordulás)
egész osztás, valós osztás
lebegőpontos típusok (pontosság, kerekítés, túlcsordulás, speciális értékek)
Egyéb tudnivalók
Alapvető tudnivalók
A programozásban azért beszélünk típusokról, mert bizonyos hibák elkerülése érdekében számon kell tartanunk, hogy azok az adatok, amikkel a programunk dolgozik, milyen típusúak.
Típus
A számítástechnikában a típus technikailag azt jelenti, hogy a memóriában lévő adatokat hogyan értelmezzük. Például egy valós szám esetén valahogy így lehetne elképzelni: az első bit az előjel, a következő néhány bit a kitevő, a maradék bitek pedig a hatványozatlan szám. Ezekkel az alacsonszintű
Vagy például amikor egy karaktert tárolunk, valójában egész számokat tárolunk, és egy úgynevezett karaktertábla írja le, hogy melyik számnak milyen karakterérték felel meg (például az ASCII tábla szerint a 97 jelenti a kis a betűt). Egy szöveg valójában több karakterérték egymás mögé rakva a memóriában, amiket technikailag tömbökben tárolunk (a tömbökről későbbi tananyagrész szól), egy dátum pedig valójában három darab szám, amit általában osztályok/objektumok segítségével valósítunk meg, satöbbi.
Alaptípusok és alaptípusú változók
Az alaptípusok (fundamental types), vagy más néven beépített típusok (built-in types), vagy egyszerű típusok (primitive types) olyan típusok, amik megtalálhatóak a nyelvben, anélkül, hogy bármit is includeolnunk kellene, illetve nem bonthatók további típusokra, azaz nem összetett típusok.
A C++ nyelvben az alaptípusú változók beépítettek is (nem kell őket includeolni) és egyszerűek is (nem bonthatók további típusokra). Ez nem biztos, hogy más programozási nyelvekben is így van. Elképzelhető, hogy valamelyik nyelvben includeolás nélkül elérhető például a string típus (sőt, például Javascriptben a string típus nem bontható további típusokra, mivel Javascriptben nincs külön karakter típus, Javascriptben egyetlen karakter is string).
- stackoverflow.com - difference between fundamental vs built-in types
- stackexchange.com - primitive types vs fundamental types
A C++ nyelvben használható alaptípusok teljes listáját például itt találjuk meg:
- cppreference.com - fundamental types
- cplusplus.com - fundamental data types
- docs.microsoft.com - built-in types
- eel.is - fundamental types
Ezek közül nem mindegyik lehet változók típusa, például void típusú változót nem lehet létrehozni, a void típus pointerekre vagy függvények visszatérési értékére vonatkozhat.
A leggyakoribb alaptípusú változók, amiket az első példaprogramjainkban használunk:
bool, char, int, double.
A C++ nyelvben nem tekintjük alaptípusoknak az alaptípusokból létrehozott dolgokat, mint például tömbök, függvények, pointerek, referenciák, satöbbi. Ezeket összetett típusoknk (compound types) nevezzük a C++ nyelvben. Ezek teljes listáját ebben a felsorolásban tekinthetjük meg:
Elképzelhető, hogy valahol úgy fogalmaznak, hogy például egy tömbnek van valamilyen típusa, amely típus lehet alaptípus is (pl. int), ahelyett hogy az int tömb az egy összetett típus. Erről biztos jókat lehetne vitatkozni, vannak olyan programozási nyelvek, ahol ez így is van, én ezt nem tekinteném hibának.
Az std::is_fundamental</*tipus*/>::value; utasítással vizsgálhatjuk meg, hogy a < > jelek között megadott típus alaptípusú-e, illetve az std::is_compound</*tipus*/>::value; utasítással pedig azt, hogy összetett típus-e. Ezeket az utasításokat akkor használhatjuk, ha includeoljuk a C++ standard library type_traits header fájlját. Például:
//is fundamental?
#include <iostream>
#include <string>
#include <type_traits>
int main() {
std::cout.setf(std::ios::boolalpha);
std::cout << "int type is fundamental?\n" << std::is_fundamental<int>::value << '\n';
std::cout << "std::string type is compound?\n" << std::is_compound<std::string>::value << '\n';
}Típusminősítők (qualifiers)
Angolul CV qualifiersnek, illetve const and volatile qualifiersnek is szokták nevezni őket.
const
A const kulcsszóról már volt szó korábban, noha nem csak változók esetén használhatjuk, hanem többféle kontextusban, lényegében azt jelenti, hogy valaminek az értékét nem szeretnénk megváltoztatni, és ha ennek megkísérlésére mégis sor kerülne, akkor fordítási hibát kapunk.
volatile
A volatile kulcsszó segítségével arra utasítjuk a fordítót, hogy egy adott változóval kapcsolatban ne végezzen optimalizálást. Ebben a tananyagban ezzel nem foglalkozunk részletesen. Például itt található róla néhány tudnivaló:
- cppreference.com - cv type qualifiers
- Jason Turner - volatile keyword
- isocpp.org - rare proper uses of volatile
- stackoverflow.com - when do we use volatile
- JF Bastien - Deprecating volatile (videó)
Típusmódosítók (modifiers)
Méret
A számítógép memóriája véges, ezért például az egész szám-, vagy valós szám típusú változóknak nem lehet túl nagy vagy túl kicsi (sok számjegyből álló negatív- vagy nullához túl közeli tört) szám az értékük. Nagyon nagy számok (bignum, bigint) tárolása C++ nyelvben például libraryk segítségével oldható meg. Bár ez elsőre zavarónak tűnhet, a helyzet az, hogy a programozásban általában nincs szükség nagyon nagy számok (például 100 vagy 1000 jegyű számok) tárolására. Ez kicsit ahhoz hasonlítható, hogy a mai átlagos számológépekbe sem tudunk bármennyi számjegyet beírni, a hétköznapi számításaink elvégzéséhez mégis megfelelőek.
A C++ nyelv alaptípusai között különböző méretű egész szám-, illetve valós szám típusok léteznek, amiknek a nagy részét típusmódosítókkal használhatjuk.
- short int, long int, long long int
- long double
Például egy short int típusú változó kevesebb helyet foglal a számítógép memóriájában, mint egy int típusú változó, de a legnagyobb szám, ami értékül adható egy short int típusú változónak, sokkal kisebb (a mai átlagos számítógépeken jó eséllyel 32767), mint amekkora szám egy int típusú változónak lehet az értéke (a mai átlagos számítógépeken jó eséllyel 2147483647).
A típusmódosítókat a változók definiálásakor (létrehozásakor) kell megadni. Például:
short int variable_example_1 = 0;
long long int variable_example_2{4LL};
long double variable_example{1.3L};A C++ nyelvben nem létezik short double, a double-nél szűkebb tartományon értelmezett valós szám típus a float. A float nem típusmódosító, hanem egy külön típus, mint a double.
A C nyelv terminológiájában esetleg talán előfordul, hogy a double típust long floatnak nevezik, de kulcsszó szinten csak float és double létezik a C és a C++ nyelvben is.
Előjel
Egész szám típusú változók esetén az unsigned típusmódosítóval kizárólag nem negatív számok tárolhatóak egy adott változóban. Gondolhatnánk, hogy ennek elvileg az lenne az előnye, hogy ha biztosan tudjuk, hogy nem kell negatív számokat tárolnunk, akkor a nagyobb pozitív számokat is tárolhatunk egy adott változóban.
A mai átlagos számítógépeken egy int típusú változóban jó eséllyel 2147483647 a legnagyobb tárolható szám, egy unsigned int típusú változóban pedig 4294967295. Könnyen belátható, hogy ez miért van így, az int típusban a mai átlagos számítógépeken -2147483648 és 2147483647 közötti számértékek tárolhatóak, akkor ha egy ugyanekkora méretű változóban csak pozitív számokat tárolunk (és a nullát), akkor 0-tól kezdve a nagyjából kétszer akkora számértékig (4294967295), mint az int lehetséges legnagyobb értéke (2147483647) tárolhatjuk a számokat.
Az unsigned típusmodósítót a változók definiálásakor (létrehozásakor) kell megadni. Példa:
#include <iostream>
int main() {
unsigned int unsigned_example{};
std::cout << "kerem adjon meg egy nem negativ szamot:\n";
std::cin >> unsigned_example;
std::cout << "a beolvasott ertek: " << unsigned_example << '\n';
}Az unsigned típusmódosító nem használható valós szám típusú változókhoz (float, double, long double).
//error
int main() {
unsigned double example;
}Létezik signed típusmódosító is, ami ugyanazt jelenti, mintha nem írnánk semmit helyette az egész szám típusú változókhoz. Például a signed int ugyanazt jelenti, mint az int.
Fontos: hibát okozhat, ha egy kifejezésben egyszerre használunk unsigned és signed típusokat. Az a tapasztalat, hogy ha egy program forráskódjában usigned típust használunk, az valahogy össze fog keveredni a signed típusokkal, ezért azt javasolják, hogy unsigned típusokat csak nagyon ritka esetekben (pl. bitsorozatok tárolására) használjunk, és alapvetően a signed típusokat használjuk számértékek tárolásához és hétköznapi számműveletekhez (pl. összeadás, szorzás, átlagszámítás, satöbbi).
(Ha egy változóban csak pozitív számokat szeretnénk tárolni (pl. ne lehessen -2 terméket rendelni), azt input validationnel tudjuk megoldani, ami későbbi tananyagrész témája.)
//error
#include <iostream>
int main() {
unsigned int unsigned_example = 1;
int signed_example = 2;
std::cout << unsigned_example - signed_example << '\n';
}//error
#include <iostream>
int main() {
std::cout << 1u - 2 << '\n';
std::cout << 1 - 2u << '\n';
}A hibának az az oka, hogy ha valahol egy kifejezésbe signed és unsigned int kerül, akkor nem az unsigned int konvertálódik (signed) intté, hanem fordítva, a (signed) int konvertálódik unsigned intté (más programozási nyelvekben ez nem biztos, hogy így van), ami könnyen okoz hibát.
Ez persze megkerülhető lenne explicit konverzióval, viszont azt meg sajnos könnyű elfelejteni, főleg akkor, ha egy kiszámítandó eredményt sok-sok függvény adogat át egymásnak, ezért inkább azt javasolják, hogy általában ne is használjunk unsigned típusokat.
#include <iostream>
int main() {
unsigned int unsigned_example = 1;
int signed_example = 2;
std::cout << static_cast<int>(unsigned_example) - signed_example << '\n';
}- isocpp.org - Don’t mix signed and unsigned arithmetic
- isocpp.org - Use unsigned types for bit manipulation
- isocpp.org - Use signed types for arithmetic
- isocpp.org - Don’t try to avoid negative values by using unsigned
- learncpp.com - Unsigned integers, and why to avoid them
- Jon Kalb - unsigned: A Guideline for Better Code (videó)
- John McFarlane: Signed Integers Faster and Corrector (videó)
Típusmódosítók a literálokban
A literálok esetén felmerülhet, hogy ha leírjuk például azt, hogy 128, akkor például az int típusra vagy az unsigned int típusra, vagy a long int típusra, stb gondoltunk. Az ezekre vonatkozó jelölések (suffixek) a következőek:
int típusú:
0128unsigned int típusú:
128ulong int típusú:
128Llong long int típusú:
128LLunsigned long long int típusú:
128uLLfloat típusú:
1.2fdouble típusú:
1.21.01.0.0long double típusú:
1.2LA literálokban szereplő típusmódosítók esetén nem számít a kis- és nagybetű, de például L helyett nem érdemes l-t írni, mert egyes betűtípusok esetén első ránézésre összekeverhető az 1-es karakterrel.
A short intnek nem létezik jelölése literálok esetén.
Fontos kihangsúlyozni, ha tizedespont nélkül írunk le egy egész számot a forráskódba (pl. 0, 4, -128), akkor annak a típusa int. Ha azt szeretnénk, hogy double legyen egy egész szám literálnak a típusa, akkor használjunk tizedespontot (például 0.0, 4.0, -128.0).
- cppreference.com - integer literal
- cppreference.com - floating point literal
- learncpp.com - literals
Bár a C++ nyelvben a string literálok nem tartoznak az alaptípusok közé (eleve a stringek sem), a string literálokban is találkozhatunk a fentiekhez hasonló jelölésekkel (amik jellemzően a string literálok elején szerepelnek). Ezek jellemzően a különböző karakterkódolást jelölik, ami az éketezes karakterek és egyéb nyelvek ABC-i karaktereinek tárolása esetén lehetnek fontosak.
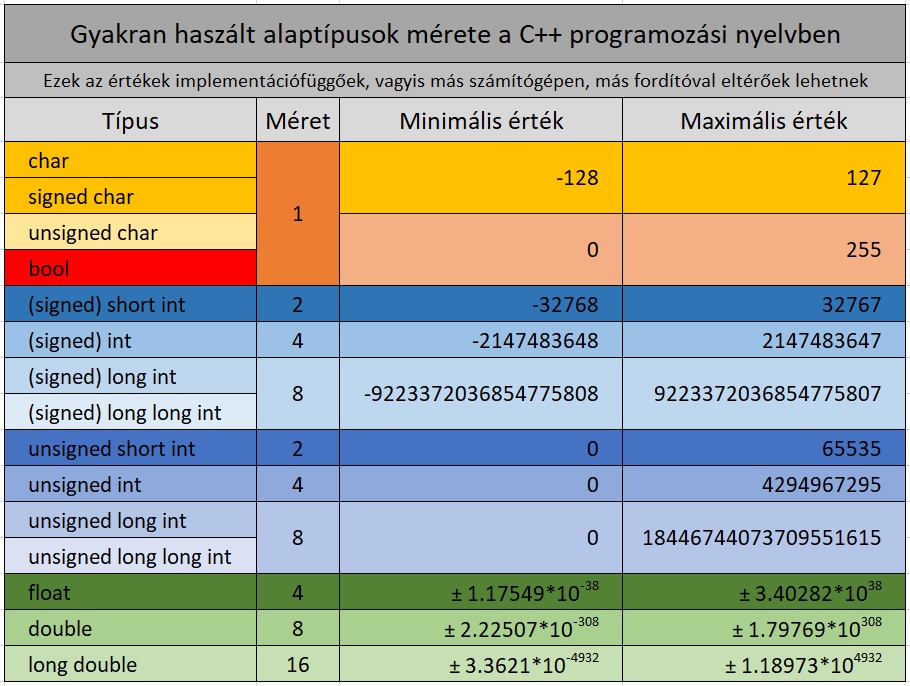
Implementációfüggő méretek
A C++ nyelvben a leggyakrabban használt alaptípusok mérete implementációfüggő, azaz különböző számítógéptípusonként és különböző fordítók használata esetén eltérhet. Az átlagos felhasználói számítógépek között ebben jó eséllyel csak kisebb különbségek lehetnek. Az int, float, double, satöbbi típusok méretét illetően jelentős különbség például a 32 bites processzorú és 64 bites processzorú számítógépek között van, illetve esetleg akkor térhetnek jelentősen a megszokott értékektől, ha például az átlagos felhasználói számítógépektől jelentősen különböző számítógépeken/eszközökön programozunk (pl. mikrokontrollerek vagy mainframe számítógépek).
Legkisebb és legnagyobb értékek
Például ezzel a példaprogrammal írathatjuk ki a parancssorba, hogy mi a legkisebb, illetve legnagyobb érték, ami az int, float, double típusú változóknak értékül adható. (A main függvényen belül az indentálás a hosszú sorok miatt lett mellőzve).
//min, max of int, float, double
#include <iostream>
#include <limits>
int main() {
std::cout << "The minimum and maximum values of int, float, double types\n";
std::cout << "This can be different on/with other computer/compiler\n";
std::cout.put('\n');
std::cout << "unsigned short int\n";
std::cout << std::numeric_limits<unsigned short int>::min() << '\n';
std::cout << std::numeric_limits<unsigned short int>::max() << '\n';
std::cout.put('\n');
std::cout << "unsigned int\n";
std::cout << std::numeric_limits<unsigned int>::min() << '\n';
std::cout << std::numeric_limits<unsigned int>::max() << '\n';
std::cout.put('\n');
std::cout << "unsigned long int\n";
std::cout << std::numeric_limits<unsigned long int>::min() << '\n';
std::cout << std::numeric_limits<unsigned long int>::max() << '\n';
std::cout.put('\n');
std::cout << "unsigned long long int\n";
std::cout << std::numeric_limits<unsigned long long int>::min() << '\n';
std::cout << std::numeric_limits<unsigned long long int>::max() << '\n';
std::cout.put('\n'); std::cout.put('\n');
std::cout << "short int\n";
std::cout << std::numeric_limits<short int>::min() << '\n';
std::cout << std::numeric_limits<short int>::max() << '\n';
std::cout.put('\n');
std::cout << "int\n";
std::cout << std::numeric_limits<int>::min() << '\n';
std::cout << std::numeric_limits<int>::max() << '\n';
std::cout.put('\n');
std::cout << "long int\n";
std::cout << std::numeric_limits<long int>::min() << '\n';
std::cout << std::numeric_limits<long int>::max() << '\n';
std::cout.put('\n');
std::cout << "long long int\n";
std::cout << std::numeric_limits<long long int>::min() << '\n';
std::cout << std::numeric_limits<long long int>::max() << '\n';
std::cout.put('\n'); std::cout.put('\n');
std::cout << "float\n";
std::cout << std::numeric_limits<float>::lowest() << '\n';
std::cout << std::numeric_limits<float>::max() << '\n';
std::cout << "smallest positive:\n";
std::cout << std::numeric_limits<float>::min() << '\n';
std::cout.put('\n');
std::cout << "double\n";
std::cout << std::numeric_limits<double>::lowest() << '\n';
std::cout << std::numeric_limits<double>::max() << '\n';
std::cout << "smallest positive:\n";
std::cout << std::numeric_limits<double>::min() << '\n';
std::cout.put('\n');
std::cout << "long double\n";
std::cout << std::numeric_limits<long double>::lowest() << '\n';
std::cout << std::numeric_limits<long double>::max() << '\n';
std::cout << "smallest positive:\n";
std::cout << std::numeric_limits<long double>::min() << '\n';
}- cppreference.com - range of values
- stackoverflow.com - what are the actual min/max values for float and double
Technikailag a char típusokban is számokat tárolunk. A lentebbi példában láthatjuk, hogy hogyan írathatjuk ki a legkisebb és legnagyobb tárolható számértéket a char típusokban. A char típushoz kapcsolódó egyéb tudnivalókról kicsit lentebb lehet olvasni.
//min, max of char
#include <iostream>
#include <limits>
int main() {
std::cout << "The minimum and maximum values of char types\n";
std::cout << "This can be different on/with other computer/compiler\n";
std::cout.put('\n');
std::cout << "char\n";
std::cout << static_cast<int>(std::numeric_limits<char>::min()) << '\n';
std::cout << static_cast<int>(std::numeric_limits<char>::max()) << '\n';
std::cout.put('\n');
std::cout << "signed char\n";
std::cout << static_cast<int>(std::numeric_limits<signed char>::min()) << '\n';
std::cout << static_cast<int>(std::numeric_limits<signed char>::max()) << '\n';
std::cout.put('\n');
std::cout << "unsigned char\n";
std::cout << static_cast<int>(std::numeric_limits<unsigned char>::min()) << '\n';
std::cout << static_cast<int>(std::numeric_limits<unsigned char>::max()) << '\n';
}Hasonlóan kiírathatjuk a bool típusnak megadható értékeket is.
std::cout << std::numeric_limits<bool>::min()<< '\n';
std::cout << std::numeric_limits<bool>::max()<< '\n';Ami nem teljesen igaz, mert ha nem adunk kezdőértéket egy bool típusú változónak, akkor lehet 0 és 255 közötti egész szám az értéke. Lásd:
Példa
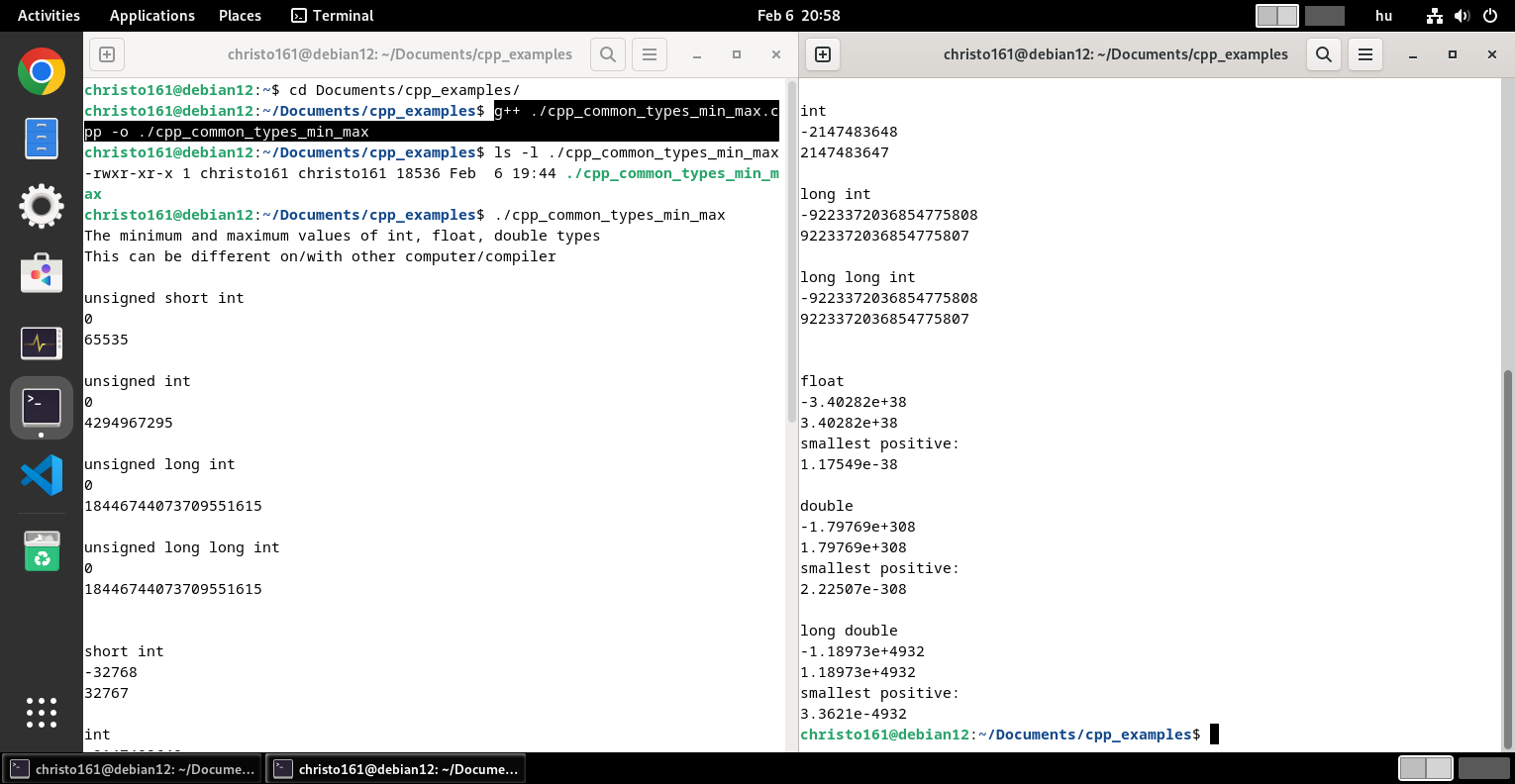
- cppreference.com - fundamental types, range of values
- learn.microsoft.com - Data Type Ranges
- cplusplus.com - Variables, Data Types, Fundamental data types
Egyéb típusok
Egyéb típusok minimális és maximális értékét is kiírathatjuk:
std::cout << std::numeric_limits<size_t>::min()<< '\n';
std::cout << std::numeric_limits<size_t>::max()<< '\n';std::cout << std::numeric_limits<std::streamsize>::min()<< '\n';
std::cout << std::numeric_limits<std::streamsize>::max()<< '\n';Bár arról már volt szó, hogy az std::string nem alaptípus, azért kiegészítésképpen szerepelhet ebben a felsorolásban, hogy hogyan kérdezhetjük le, hogy hány karakter tárolható egy std::stringben:
#include <iostream>
#include <string>
int main() {
std::string example;
std::cout << example.max_size();
}Egyéb információk
Az std::numeric_limits segítségével mindenféle részletekbemenő információkat lekérdezhetünk az alaptípusú változókról.
Például azt, hogy hány számjegy pontosság garantált egy float, double vagy long double típusú változó esetén:
std::cout << std::numeric_limits<float>::digits10 << '\n';
std::cout << std::numeric_limits<double>::digits10 << '\n';
std::cout << std::numeric_limits<long double>::digits10 << '\n';Hogy mit jelent a float, double és long double típusok pontossága, arról az "egyes típusokról bővebben" alcímnél találhatunk leírást és példaprogramokat.
Vagy például, hogy mennyi a számjegyek tárolásra használt bitek száma (pl. a signed típusoknál 1-el kevesebb, mint az unsigned típusoknál, mivel 1 bitet az előjel tárolására használunk):
std::cout << std::numeric_limits<signed int>::digits << '\n';
std::cout << std::numeric_limits<unsigned int>::digits << '\n';Méret lekérdezése
Az, hogy hány különböző érték tárolható egy változóban, meghatározza egyúttal azt is, hogy az adott változó mekkora helyet foglal a memóriában.
A sizeof operátorral kérdezhetjük le az egyes típusok méretét.
//sizeof example
#include <iostream>
int main() {
std::cout << "The size of some fundamental types in bytes\n";
std::cout << "This can be different on/with other computer/compiler\n";
std::cout.put('\n');
std::cout << "char: " << sizeof(char) << '\n';
std::cout.put('\n');
std::cout << "bool: " << sizeof(bool) << '\n';
std::cout.put('\n');
std::cout << "short int: " << sizeof(short int) << '\n';
std::cout << "int: " << sizeof(int) << '\n';
std::cout << "long int: " << sizeof(long int) << '\n';
std::cout << "long long int: " << sizeof(long long int) << '\n';
std::cout.put('\n');
std::cout << "float: " << sizeof(float) << '\n';
std::cout << "double: " << sizeof(double) << '\n';
std::cout << "long double: " << sizeof(long double) << '\n';
std::cout.put('\n');
}A sizeof által megadott méretek bájtban értendők. Terjengenek ilyesmi tévhitek, hogy a char típus mérete nem mindig 1 bájt, hanem az 1 valójában egy egységnek értendő, és bizonyos szuperszámítógépeken a char típus lehet nagyobb is mint 1 bájt. Megnézhetjük a hivatalos C++ dokumentációt az isocpp.org oldalon:
- isocpp.org - sizeof(char) is always 1
- isocpp.org - unit of sizeof is bytes
- isocpp.org - rules of bytes, chars, characters
A sizeof operátorral nem csak alaptípusú változók méretét kérdezhetjük le, hanem például tömbök és objektumok méretét is.
size_t
A sizeof operátor, valamint az std::string vagy a későbbiekben tárgyalt std::vector size vagy length tagfüggvénye, vagy például a C nyelvből átvett strlen függvény visszatérési típusa size_t, másképp fogalmazva size_t típusú eredményt adnak vissza.
A size_t típus valójában egy alias (a C++ nyelv terminológiája szerint egy typedef), vagyis egy már meglévő típus másképp történő elnevezése. Viszont különböző számítógéptípusokon, különböző fordítókat használva eltérő lehet az, hogy pontosan melyik típus typedefje a size_t.
A mai átlagos felhasználói számítógépeken a size_t jó eséllyel az unsigned long int típusnak felel meg.
//type behind size_t alias
#include <iostream>
#include <cstdint>
#include <typeinfo>
int main() {
std::cout << "size_t typeid: " << typeid(size_t).name() << '\n';
std::cout << "unsigned long int typeid: " << typeid(unsigned long int).name() << '\n';
}Fontos: mivel a size_t típus valójában egy unsigned típus, ezért arra is ügyelnünk kell, hogy ne használjuk signed típusokkal egy kifejezésben. Tipikusan például for ciklusokban fordulhat elő, hogy a ciklusváltozó string_example.size()-ig veszi fel az értékeket, viszont ha a ciklusváltozót nem size_t típusúként hozzuk létre, hanem (signed) intként, akkor az hibát okozhat.
Egy nagyon egyszerű szemléltető példa:
//error
#include <iostream>
int main() {
std::cout << sizeof(short int) - 3;
}Az alaptípusok mérete a C++ szabvány szerint
A C++ szabvány nem határozza meg pontosan, hogy az egyes alaptípusú változók mérete mekkora legyen, mivel C++ nyelven különböző számítógéptípusokon is programozhatunk, különböző fordítókat és operációs rendszereket használva. A különböző rendszereken más lehet a megfelelő.
Amiben viszont biztosak lehetünk, hogy ha olyan fordítót használunk, ami betartja a C++ szabványt, akkor ezek a feltételek biztosan teljesülnek:
- 1 == sizeof(char) <= sizeof(short int) <= sizeof(int) <= sizeof(long int)
- 1 <= sizeof(bool) <= sizeof(long int)
- sizeof(char) <= sizeof(wchar_t) <= sizeof(long int) <= sizeof(long long int)
- sizeof(float) <= sizeof(double) <= sizeof(long double)
- sizeof(int) == sizeof(signed int) == sizeof(unsigned int) és ugyanez short int, long int, valamint long long int esetén is érvényes
A == jel itt ugyanakkorát (egyenlőt) jelent, a <= jel pedig legfeljebb akkorát (kisebb vagy egyenlőt). Például azt mondhatjuk, hogy a C++ szabvány szerint a short int lehet akár ugyanakkora is valamilyen rendszeren, mint az int, de nem lehet nála nagyobb.
Elképzelhető, hogy egyes típusok mérete/pontossága megegyezik bizonyos rendszereken például a double és long double típusok ugyanakkora méretűek a Microsoft fordítójával.
Fix méretű int típusú változók
A C++11-es szabványtól kezdve elérhetőek olyan int típusok, amiknek a mérete minden rendszeren, minden fordítóval ugyanakkora. Például int8_t, int16_t, int32_t, int64_t, satöbbi, melyeket a C++ standard library cstdint header fájljának includeolásával használhatunk.
Ha a forráskódunkból különböző rendszereken szeretnénk futtatható programot létrehozni, akkor ezeknek a használata esetleg megfontolandó lehet, de általában a hagyományos int típus használata teljesen megfelelő, sokan nem javasolják ezeknek a fix méretű int típusoknak a használatát, csak indokolt esetekben.
#include <iostream>
#include <cstdint>
int main() {
std::cout << "kerem adjon meg egy -2147483648 es 2147483647 kozotti szamot:\n";
int32_t example;
std::cin >> example;
std::cout << "a beolvasott szamertek: " << example << '\n';
}Érdemes lehet tudni, hogy ezek a fix méretű típusok valójában aliasok (typedefek) a hagyományos alaptípusokra. Hogy pontosan milyen típusokra, az viszont különböző rendszereken eltérhet. Átlagos felhasználói számítógépeken például az int32_t az int típussal egyezik, az int16_t a short int típussal, az int8_t a signed char típussal, satöbbi. A std::cout << typeid(/*kifejezes*/).name() << '\n'; utasítással kiírathatjuk a zárójelek között megadott kifejezés típusát, mely kifejezés akár egy típus is lehet. Így láthatjuk, hogy például az int8_t típus mögött valójában milyen típus van. A gcc és clang fordítókkal elkészített futtatható programban a kiírt típusnév jó eséllyel csak egy rövidítés lesz, a Microsoft C++ fordítója (msvc) talán kiírja a teljes típusneveket.
#include <iostream>
#include <cstdint>
#include <typeinfo>
int main() {
std::cout << "int8_t:\t\t" << typeid(int8_t).name() << '\n';
std::cout << "signed char:\t" << typeid(signed char).name() << '\n';
std::cout << "int16_t:\t" << typeid(int16_t).name() << '\n';
std::cout << "short int:\t" << typeid(short int).name() << '\n';
std::cout << "int32_t:\t" << typeid(int32_t).name() << '\n';
std::cout << "int:\t\t" << typeid(int).name() << '\n';
}Az int8_t típus esetén előfordulhat, hogyha hagyományos módon használjuk, úgy fog viselkedni, mint a char típus, pl. ha 48-at adunk értékül egy int8_t típusú változónak, és ezt követően ki akarjuk íratni az értékét, akkor a kiírt érték 0 lesz, mivel az ASCII táblában a negyvennyolcadik karakter a 0. Ha viszont a kiíratásnál átkonvertáljuk int típusúvá, akkor nem az ASCII táblának megfelelő érték lesz kiírva, hanem a ténylegesen eltárolt számérték.
#include <iostream>
#include <cstdint>
int main() {
int8_t example = 48;
std::cout << "ascii character: " << example << '\n';
std::cout << "number: " << static_cast<int>(example) << '\n';
}- cppreference.com - fixed width integer types
- belaycpp.com - about sizes
- quora.com - is using int32_t preferret to using int?
Egyéb char típusú változók
Említés szintjén szerepelhetnek ebben a tananyagrészben a wchar_t, a C++11-es vagy újabb szabványtól elérhető chart16_t és char32_t típusok, illetve a C++20-as szabványtól a char8_t típus is. Például ékezetes karakterek, vagy a latin abc-től eltérő abc-k (pl. görög, orosz, japán, kínai) karaktereinek tárolásához használhatóak.
- microsoft.com - char, wchar_t, char16_t, char32_t
- ducmanhphan.github.io - how to use char, wchar_t, char16_t, char32_t
- cppreference.com - char8_t
- stackoverflow.com - is char8_t the same as old char
Továbbá azt is érdemes lehet tudni, hogy az std::string típushoz hasonlóan ezekből a karakter típusokból is használhatunk string típusokat (pl. std::wstring, std::u8string, std::u16string, std::u32string).
Hogyan válasszunk a különböző típusok közül?
Általában két dolgot lehet mérlegelni, amikor eldöntjük, hogy bizonyos adatokat/értékeket milyen típusú változóban szeretnénk tárolni. Az egyik, hogy milyen műveleteket szeretnénk végezni az adott adattal/értékkel, a másik, hogy mennyi a költsége az adott típusnak (pl. egy std::string használata sokkal lassabb, több memóriát igényel, mint mondjuk egy int típus).
short int, int, long int, long long int
Általában érdemes a hagyományos int típust választani, mert a fordító azzal tud a legoptimálisabb futtatható programot előállítani.
Átlagos felhasználói számítógépekre írt programokban nem érdemes spórolni azzal, hogy mindenütt short intet használunk, ahol tudjuk, hogy abba is beleférnek a programunkban használt számértékek. Esetleg kivétel lehet, ha tömegesen használunk short inteket (pl. százezer, vagy milliós nagyságrendű elemszámmal rendelkező tömb vagy std::vector esetén).
long intet vagy long long intet alapvetően indokolt esetben használjunk, ha tudjuk, hogy a programunkban használt számértékek nem férnek bele az int típusba, illetve esetleg akkor, ha olyan rendszerre készítünk programot, ahol az int típus kisebb tartományon van értelmezve, mint a mai átlagos felhasználói számítógépeken.
- isocpp.org - choosing int size
- stackoverflow - why int should be preferred
- Dan Saks: Choosing the Right Integer Types in C and C++ (videó)
float, double, long double
Az int típushoz hasonlóan általában ezek közül is érdemes nem a kisebbet (float) vagy a nagyobbat (long double) választani, ami itt a doublet jelenti, mivel a fordító azzal tud a legoptimálisabban futtatható programot előállítani.
float típus használatával általában csak akkor érdemes spórolni, ha nem átlagos felhasználói számítógépre készítünk programot, vagy ha tömegesen szeretnénk float típusú értékeket használni.
A long double használata szintén csak indokolt esetben érdemes, viszont azt érdemes tudni, hogy bizonyos rendszereken (pl. a Microsoft fordítójával) a mérete a double típuséval egyezik.
Jason Turner: cppbestpractices - prefer double to float
egész szám, valós szám
A választás alapvetően nyilvánvalónak tűnhet, de vannak olyan esetek, amik kezdő programozók számára nem biztos, hogy magától értetődőek.
Ne használjunk float, double, long double típusokat olyan számításokhoz, ahol nem megengedettek a kerekítések (pl. pénzügyi számítások).
Lehetőleg ne használjunk float, double, long double típusokat összehasonlításokhoz (nagyobb, nagyobbegyenlő, egyenlő-e), amik jellemzően elágazásokban, ciklusokban fordulnak elő.
- isocpp.org - why doesn't floating-point comparsion work?
- isocpp.org - why is floating point so inaccurate?
számok szövegként
Elképzelhető, hogy egyes esetekben érdemes lehet számokat szövegként (például std::string típussal) tárolni, tipukusan például szövegekkel végezhető műveletekhez. Például:
- karakterek sorrendjének megfordítása (reverse)
- összefűzés (konkatenáció)
- egy szám bizonyos számjegyeinek kiválasztása (pl. dátumok, irányítószámok esetén)
Az egyes típusokról bővebben
char
A char típusú változókban valójában számokat tárolunk, csakúgy mint egy int típusban, de amikor std::cout<< utasítással kiíratjuk az értékét, nem a számérték íródik ki, hanem a neki megfelelő karakter. Hogy milyen számértéknek pontosan milyen karakter felel meg azt az ASCII táblából tudhatjuk meg.
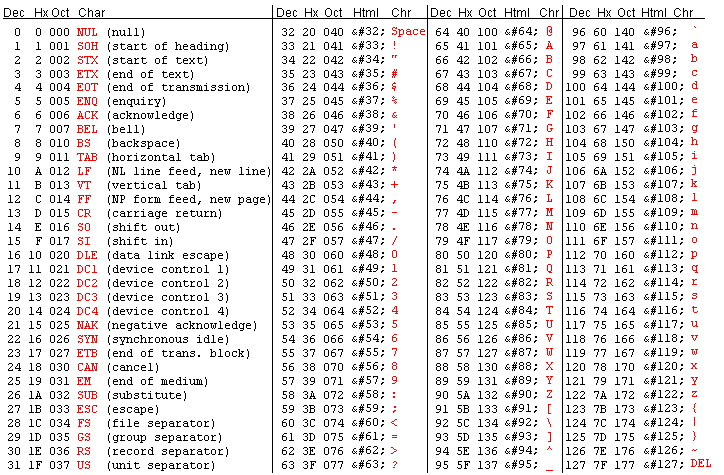
Az ASCII tábla
Ha például egy char típusú változónak 97-et adunk értékül, az olyan, mintha csak az 'a' literált adtuk volna értékül neki, mivel az a betű ASCII kódja 97.
//ascii code example
#include <iostream>
int main() {
char example = 97;
std::cout << example << '\n';
}Ha esetleg nem az ASCII kódnak megfelelő karaktert szeretnénk kiíratni, hanem a számértéket, akkor vagy át kell konvertálnunk egész szám típusúvá. Ezt többféleképpen is megtehetjük:
char example = 97;
std::cout << static_cast<int>(example) << '\n';char example = 97;
std::cout << +example << '\n';Akár azt is megtehetjük, hogy kezdőértéknek karaktert adunk meg, majd a kiíratáskor átkonvertáljuk számmá, így a karakter ASCII kódját kapjuk meg:
//ascii code example
#include <iostream>
int main() {
char example = '\n';
std::cout << static_cast<int>(example) << '\n';
}Az ASCII táblában 0-tól 31-ig tartó ASCII kódnak, illetve a 127-es ASCII kódnak megfelelő karakterek úgynevezett vezérlőkarakterek (nem nyomtatható karakterek).
Az ASCII táblában 32-től 126-ig tartó ASCII kódnak megfelelő karakterek tartalmazzák az angol abc kis- és nagybetűit, 0-9-ig a számokat, illetve a leggyakrabban használt írásjeleket.
Érdemes arra is figyelni, hogy a '0' számmá konvertálva 48, az '1' számmá konvertálva 49, satöbbi. A '\0' speciális karakter számmá konvertálva 0.
//ascii code example
#include <iostream>
int main() {
std::cout << "'0' converted to int: " << static_cast<int>('0') << '\n';
std::cout << "'\\0' converted to int: " << static_cast<int>('\0') << '\n';
}Az ASCII tábla nem tartalmaz ékezetes karaktereket, mert olyan régen találták ki, hogy akkoriban még nem tartották fontos szempontnak, hogy az ékezetes karaktereket is meg lehessen jeleníteni az akkor még többnyire csak Amerikában forgalmazott számítógépeken. Többféle megoldás is létezik az ékezetes karakterek megjelenítésére, például bővített ASCII tábla, vagy más kódtáblák használata (pl. utf-8), de a C++ nyelvben az ékezetes karakterek kezelése sajnos nem annyira magátólértetődő, mint egyéb programozási nyelvekben.
A char típust tulajdonképpen kisebb számok tárolására is lehetne használni (más programozási nyelvekben (pl. Pascal, C#) előfordulhat, hogy erre külön típus létezik, amit jellemzően byte-nak hívnak), de ennek esetleg akkor lehet létjogosultsága, ha olyan rendszeren programozunk, ahol nagyon korlátozottak az erőforrások, illetve átlagos felhasználói számítógépeken tömeges tárolás esetén.
Egy korábbi tananyagrészben már volt szó arról, hogy ha a felhasználótól kérjük be egy char típusú változó értékét a parancssorból, akkor ha a felhasználó több karaktert ír be, csak az első karakter lesz értékül adva a char típusú változónak, a további karaktereket a további bekérések fogják feldolgozni, ezért ha azt szeretnénk, hogy egyetlen char típusú változóba a felhasználótól bekért többjegyű számnak ne csak az első karaktere legyen beolvasva, akkor először egy int típusú változóba kérjük be az értéket, majd adjuk értékül a char típusú változónak.
//char as number
#include <iostream>
int main() {
signed char ch_s{};
unsigned char ch_u{};
int temp{};
std::cout << "Kerem adjon meg egy egesz szamot (-128 es 127 kozott)\n";
std::cin >> temp;
ch_s = temp;
std::cout << "Kerem adjon meg egy egesz szamot (0 es 255 kozott)\n";
std::cin >> temp;
ch_u = temp;
std::cout << "A beolvasott ertekek: " << static_cast<int> ( ch_s ) <<
", valamint: " << static_cast<unsigned int> ( ch_u ) << '\n';
}char, signed char, unsigned char
Meglepve vehetjük észre, hogy a C++ nyelvben előjeles és csak nemnegatív számok tárolására alkalmas char típusok is léteznek. De vajon mi szükség van erre, hiszen a char típust azért általában nem számok, hanem karakterek tárolására használjuk. A C++ nyelven különféle számítógéptípusokra írhatunk programokat, és voltak olyan rendszerek, ahol a signed char használatát tartották optimálisabbnak, illetve olyanok, ahol az unsigned chart.
A char típus a mai átlagos felhasználói számítógépeken jó eséllyel úgy működik, mint a signed char, de nem annak egy aliasa (typedefje), hanem egy különálló típus.
Elképzelhető, hogy vannak olyan függvények, ahol számít a különbség:
Bővebben a char, signed char és unsigned char közti különbségekről:
- cppreference.com - character types
- stackoverflow.com - what is an unsigned char
- stackoverflow.com - what does it mean for a char to be signed
escape karakter, speciális karakterek
A C++ nyelvben az escape karakter a \ (visszaper), amellyel karakter literálokban és string literálokban (leszámítva a raw string literálokat) azt jelöljük, hogy az utána következő karakternek speciális jelentése van.
\n - újsor, sortörés, soremelés
\t - tabulátor
\0 - string lezárókarakter
Értelemszerűen ha egy karakter literálban vagy string literálban aposztrófot, idézőjelet vagy visszaper jelet szeretnénk írni akkor a fordító csak úgy tudja eldönteni, hogy az nem a karakter literál, vagy string literál végét jelző aposztróf vagy idézőjel, vagy egy escape karakter, hogy ezek elé a karakterek elé is egy escape karaktert írunk:
\'\"\\Például:
char ch1 = '\'';
//the value of ch1: '
char ch2 = '\\';
//the value of ch2: \
std::string str1 = "\"";
//the value of str1: "
std::string str2 = "\\";
//the value of str2: \Ezek persze csak a leggyakoribb példák voltak. További példák:
Azt is érdemes lehet tudni, hogy egy stringen belül ha valahol \0 szerepel, akkor az a string végét jelenti, hiába van bármi is utána. Például:
//zero terminated string example
#include <iostream>
int main() {
std::cout << "in this example \0 this part will disappear" << '\n';
}Ha esetleg \0-t szeretnénk írni egy string részeként, akkor írjunk helyette \\0-t:
//escape sequence example
#include <iostream>
int main() {
std::cout << "in this example \\0 this part will also appear" << '\n';
}szóköz, tabulátor a standard inputról
Ha esetleg azt szeretnénk, hogy a felhasználó által a parancssorba gebépelt szóköz és tabulátor is értékül adható legyen egy char típusnak, akkor használhatjuk az std::cin.unsetf(std::ios::skipws); utasítást. Ebben a példaprogramban az első változó értékének adható szóköz vagy tabulátor, a másodiknak viszont már nem.
//' ' or '\t' as input value by std::cin
#include <iostream>
int main() {
char ch1{}, ch2{};
//space/tab/enter allowed as input
std::cin.unsetf(std::ios::skipws);
std::cin >> ch1;
//space/tab/enter are input separators
std::cin.setf(std::ios::skipws);
std::cin >> ch2;
std::cout << "ch1: '" << ch1 << "'\n";
std::cout << "ch2: '" << ch2 << "'\n";
}Ez a példaprogram pedig kiírja, hogy valóban szóköz, vagy tabulátor lett a karakter értéke. (Elképzelhető, hogy bizonyos fejlesztői környezetek, vagy online fordítók a tabulátorokat átalakítják szóközökké.)
#include <iostream>
int main() {
char ch{};
//space,tab,enter allowed as input
std::cin.unsetf(std::ios::skipws);
std::cin >> ch;
std::cout << "ch: '" << ch << "'\n";
std::cout.setf(std::ios::boolalpha);
std::cout << "ch value is space? " << (ch == ' ') << '\n';
std::cout << "ch value is tabulator? " << (ch == '\t') << '\n';
std::cout << "ch value is newline? " << (ch == '\n') << '\n';
}std::string típusok esetén ez a módszer nem használható. Az std::cin az std::cin.unsetf(std::ios::skipws); utasítást követően is csak az első szóközig olvassa be az std::string típusok értékét. Ha nem csak az első szóközig szeretnénk beolvasni egy std::string típus értékét, hanem például a sorvége jelig, akkor használjuk a C++ standard library string header fájljában lévő getline függvényt, aminek a használata az előző tananyagrészben ismertetve lett.
short int, int, long int, long long int
Összefoglaló néven egész szám típusok, angolul integral types.
Túlcsordulás
Felmerülhet a kérdés, hogy mi történik akkor, ha az alaptípusú változókban tárolható maximális értéknél nagyobb számot próbálunk meg tárolni. Ezt legegyszerűbben úgy próbálhatjuk ki, ha mondjuk egy int vagy unsigned int típusú változó legnagyobb értékéhez hozzáadunk egyet. Ekkor a változó a benne tárolható minimális értéket veszi fel, ha kettőt adunk hozzá, akkor minimális érték + 1-et, és így tovább. Ebben a példaprogramban ez a két utasítás ugyanazt eredményezi:
//overflow test
#include <iostream>
#include <limits>
int main() {
std::cout << std::numeric_limits<unsigned int>::max()+1 << '\n';
std::cout << std::numeric_limits<unsigned int>::min() << '\n';
}Egy másik apró példaprogramban pedig kiíratjuk, hogy az int típusnak megadható maximális érték + 1 egyenlő-e az int típusnak megadható minimális értékkel:
//overflow test
#include <iostream>
#include <limits>
int main() {
std::cout.setf(std::ios::boolalpha);
std::cout << "is intmax+1 equals to intmin?\n";
std::cout << ( std::numeric_limits<int>::max()+1 ==
std::numeric_limits< int>::min() ) << '\n';
}A változókban tárolt számértékek túlcsordulása tipikus hiba a programozásban. A felhasználók számára nem biztos, hogy egyértelmű, hogy ha például az int típus legnagyobb értékénél (2147483647) nagyobb számot ad meg, akkor miért lesz abból mondjuk -2354353.
Ha nagyobb számokkal végzünk műveleteket a programjainkban akkor figyeljünk arra, hogy túlléphet-e az intnek vagy long intnek, long long intnek, esetleg long doublenek megadható maximális értékeken. Ha igen, akkor használjunk valamilyen bignum vagy bigint, esetleg safeint libraryt.
- isocpp.org - don't overflow
- isocpp.org - don't underflow
- belaycpp.com - dealing with ingeter overflows
- wikipedia.org - C++ multiple precision arithmetic libraries
- stackoverflow.com - big numbers library in c++
- stackexchange - simple method to detect overflow
Egész osztás, valós osztás
Egy lehetséges hibaforrás, ha például 5.0/2.0 helyett 5/2-t írunk, mivel az 5 és a 2 típusa int, az 5.0 és 2.0 típusa pedig double, és a C++ nyelvben az osztás máshogy van értelmezve az int (és hasonló pl. short int, long int) típusok esetén, illetve a double (és hasonló) típusok esetén.
Az egész osztás (más néven maradékos osztás) eredménye egész szám.
Például az 5 / 2 kifejezés eredménye 2
Az egész osztás maradékát a % operátorral kaphatjuk meg.
Például a 5 % 2 kifejezés eredménye 1 (mivel 2*2+1=5)
A valós osztás eredménye lehet tört szám is:
Például az 5.0 / 2.0 kifejezés értéke 2.5
Ha mind a két szám egész típusú (például int), akkor az osztás egész osztásként lesz értelmezve, ha legalább az egyik szám valós, akkor pedig valós osztásként. Ez kicsit becsapós, mert hiába tesszük bele az eredményt mondjuk egy double típusú változóba, ha az osztásban mindkét szám egész típusú, akkor az egész osztásként lesz értelmezve.
Ezen utasítás végrehajtását követően a div_result nevű változó értéke 2 lesz
//error
double div_result = 5 / 2;Ennek pedig 2,5:
double div_result = 5.0 / 2;Ha esetleg pont az lenne a cél, hogy egy double típusú változónak egészosztás eredményét adjuk értékül, akkor azt érdemes valahogy jelezni (például egy kommenttel) a kódban.
A felhasználótól bekért két számmal végzett valós- és egész osztás eredménye:
#include <iostream>
int main() {
std::cout << "Kerem adjon meg ket szamot:\n";
double d_num1{1}, d_num2{1};
std::cin >> d_num1 >> d_num2;
std::cout << "valos osztas eredmenye:\n";
std::cout << d_num1 << " / " << d_num2 << " = " << d_num1/d_num2 << '\n';
int i_num1 = d_num1, i_num2 = d_num2;
std::cout << "egesz osztas eredmenye:\n";
std::cout << i_num1 << " / " << i_num2 << " = " << i_num1/i_num2 << '\n';
std::cout << "egesz osztas maradeka:\n";
std::cout << i_num1 << " % " << i_num2 << " = " << i_num1%i_num2 << '\n';
}Ha egész osztás maradékát szeretnénk számolni, akkor az operandusoknak egész típusúnak kell lenniük (esetleg char vagy bool is lehetnek), ha legalább az egyik operandus lebegőpontos típusú, fordítási hibát kapunk. Például:
//error
std::cout << 5.0 % 3 << '\n';float, double, long double
Összefoglaló néven lebegőpontos típusok, angolul floating point types.
Pontosság
A lebegőpontos típusok számítógép memóriájában történő tárolása módja igencsak eltér az int típusokétól, ebből adódóan van egy olyan tulajdonságuk is, hogy garantált pontosság, amivel az egyes alaptípusokat összehasonlító táblázatokban is találkozhatunk.
Ez persze szintén implementációfüggő, azaz rendszerenként és fordítóként némileg eltérő lehet, de az átlagos felhasználói számítógépeken nagyjából ilyesmi értékek lehetnek: a float pontossága 6, a double pontossága 15, a long double pontossága 18.
Ez azt jelenti, hogyha például egy float típusú változónak 6 számjegynél hosszabb számot adunk értékül, akkor elképzelhető, hogy a 6. számjegy után kerekítve lesz. Persze különböző számok esetén ez akár több is lehet, mint 6. Nulla és egy közti számok esetén jellemzően jobb a pontosság, mint nagyob egészrésszel rendelkező számok esetén.
Fontos: az std::cout pontosságát is be kell állítanunk, ahhoz, hogy a különbség látható legyen. Mivel ez alapbeállítás szerint 6, így ha nem állítjuk át, akkor nagyjából a float pontosságának megfelelő lesz a double és a long double is, ha a standard outputra (jellemzően a parancssorba) íratjuk ki az értékeket.
Ezt a példaprogramot futtatva jól látható a különbség.
//float, double, long double precision test
#include <iostream>
#include <limits>
#include <string>
int main() {
const int prec_value = std::numeric_limits<long double>::max_digits10;
std::cout.precision(prec_value);
std::cout.setf(std::ios::fixed);
float f_example = 0.0123456789012345678912f;
std::cout << f_example << '\n';
double d_example = 0.0123456789012345678912;
std::cout << d_example << '\n';
long double ld_example = 0.0123456789012345678912L;
std::cout << ld_example << '\n';
}- isocpp.org - Why is floating point so inaccurate?
- C++ Data Types: Float Vs Double (videó)
- C++ floating points manipulation, How to set decimal point (videó)
- cppreference.com - setprecision
- cppreference.com - max_digits10
- stackoverflow.com - what is the purpose of max_digits10
Kerekítés
A lebegőpontos típusok velejárója a kerekítések. Például ha egy nagy számhoz hozzáadunk egy kis számot, elképzelhető, hogy az eredményben a kis szám nem fog szerepelni. Ennél a példánál az eredményben jó eséllyel nem szerepel a 0.1, de ha mégis, akkor ha az első szám tizedespontja elé írunk még néhány nullát, úgy már biztosan nem fog szerepelni, vagyis az eredmény az első szám lesz.
#include <iostream>
int main() {
std::cout.setf(std::ios::fixed);
std::cout << 10000000000000000.0 + 0.1 << '\n';
}Ha a pontosságot több sok tizedesjegyre állítjuk, akkor bizony előfordulhat, hogy ilyesmi értékeket kapunk: például a 3.01 helyett 3.0099999999999998-at, a 0.68 helyett pedig 0.68000000000000016-ot.
#include <iostream>
#include <limits>
int main(){
std::cout << 1.1 - 0.42 << '\n';
std::cout << 1.03 - 0.42 << '\n';
std::cout << 3.01 << '\n';
const int prec_value = std::numeric_limits<double>::max_digits10;
std::cout.precision(prec_value);
std::cout << 1.1 - 0.42 << '\n';
std::cout << 1.03 - 0.42 << '\n';
std::cout << 3.01 << '\n';
}Sajnos nem a túl nagy pontosság rontja el a lebegőpontos számokat, hanem a memóriában történő tárolásuk matematikai hátterének a velejárója a kerekítések és a pontatlanság. A kisebb pontosság csak elrejti ezt a problémát.
Ha például kiíratjuk a 3.01 + 0.09 kifejezés eredményét, jó eséllyel 3.1-et fogunk látni, de ha egyenlőségvizsgálattal megpróbáljuk kiértékelni, hogy a 3.01 + 0.09 kifejezés eredménye egyenlő-e 3.1-el, akkor jó eséllyel hamisat értéket kapunk.
#include <iostream>
int main() {
std::cout << 3.01 + 0.09 << '\n';
std::cout.setf(std::ios::boolalpha);
std::cout << "3.01 + 0.09 equals to 3.1?\n" << (3.01 + 0.09 == 3.1) << '\n';
}A kerekítések különbözhetnek a float és double típus esetén, ezért ügyeljünk arra, hogy ugyanazok az értékek float és double esetén nem biztos, hogy egyelőnek számítanak. Például:
#include <iostream>
int main() {
std::cout.setf(std::ios::boolalpha);
std::cout << "is float 4 equals to double 4? " << (4.0f == 4.0) << '\n';
std::cout << "is float 4.2 equals to double 4.2? " << (4.2f == 4.2) << '\n';
}Túlcsordulás, speciális értékek
Felmerülhet a kérdés, hogy lebegőpontos típusoknál is megtörténhet-e ugyanaz, mint ami az int típusoknál, hogy a lehetséges legnagyobb értékhez hozzáadunk egyet, akkor a lehetséges legkisebb értéket kapjuk.
Mivel a lebegőpotnos műveletek eredménye sok esetben kerekített érték, ezért ha hozzáadunk 1-et, 10-et, 100-at, 1000-et, stb. például mondjuk a double típusnak megadható legnagyobb értékhez, akkor a kerekítés miatt nem változik az értéke. Ha nagyságrendileg nagyobb számot (mint ami a lentebbi példában is látható) adunk hozzá a double típusnak megadható legnagyobb értékhez, akkor túlcsordulás történik.
Ekkor azonban nem ugyanaz történik, mint az int típusok esetén, hogy a legnagyobb értékből legkisebb érték lesz, hanem egy szimbolikus értéket kap a változó, legnagyobb érték esetén például végtelent (amit a cout jó eséllyel inf-ként ír ki).
inf (végtelen)
Ha tehát egy lebegőpontos típusnak adható maximális értékhez hozzáadunk egy elég nagy számot ahhoz, hogy ne történjen kerekítés, akkor végtelent kapunk. Ez talán jobb, mintha valami negatív számot kapnánk, vagy esetleg valami 0-hoz közeli számot, mivel így tudunk arra tippelni, hogy az eredmény egy nagy pozitív szám lett volna.
//overflow test with double type
#include <iostream>
#include <limits>
int main() {
std::cout.setf(std::ios::fixed);
double positive_max = std::numeric_limits<double>::max();
std::cout << "Maximum of double: \n" << positive_max << '\n';
std::cout << "Rounded to maximum of double: \n" << positive_max + 1.0 << '\n';
std::cout << positive_max +
100000000000000000000000000000000000000000000000000000.0 << '\n';
//backslash is to remove linebreaks here
std::cout << "Likely infinity: \n" << positive_max +
1000000000000000000000000000000000000000000000000000000000000\
0000000000000000000000000000000000000000000000000000000000000\
0000000000000000000000000000000000000000000000000000000000000\
0000000000000000000000000000000000000000000000000000000000000\
0000000000000000000000000000000000000000000000000.0 << '\n';
std::cout << positive_max + positive_max << '\n';
double positive_min = std::numeric_limits<double>::min();
std::cout << positive_max / positive_min << '\n';
}Végtelent nem csak így kaphatunk. Ha például 1-et elosztjuk 0-val, akkor is végtelen lesz az eredmény (int típusok esetén ez nem igaz).
//infinity test
#include <iostream>
int main() {
std::cout << 1.0/0 << '\n';
}Ha a végtelent, mint értéket szeretnénk felhasználni egy kifejezésben vagy utasításban, akkor a C++ standard library limits header fájljának includeolását követően a std::numeric_limits<double>::infinity() kifejezést használhatjuk, mint végtelent. Az is előfordulhat, hogy a C nyelvből átvett INFINITY-vel találkozunk a cmath header fájlból.
//infinity as value
#include <iostream>
#include <limits>
int main() {
double inf_example = std::numeric_limits<double>::infinity();
std::cout << inf_example << '\n';
}Az egyenlőségvizsgálat (dupla egyenlőségjel) operátorral akár le is ellenőrízhetjük, hogy egy lebegőpontos változó értéke végtelen-e.
#include <iostream>
#include <limits>
int main() {
double inf_example = std::numeric_limits<double>::infinity();
double example1 = 1.0/0;
double example2 = -1.0/0;
std::cout.setf(std::ios::boolalpha);
std::cout << "example1 is infinity?\n" << (example1 == inf_example) << '\n';
std::cout << "example2 is infinity?\n" << (example2 == inf_example) << '\n';
}-inf (minusz végtelen)
Minusz végtelent is hasonló módon kaphatunk. Esetleg arra érdemes ügyelni, hogy a std::numeric_limits<double>::min() kifejezés a nullához legközelebb eső pozitív szám, ami a double típusban ábrázolható, a legkisebb negatív számot a std::numeric_limits<double>::lowest() kifejezéssel kaphatjuk meg.
//underflow test with double type
#include <iostream>
#include <limits>
int main() {
std::cout.setf(std::ios::fixed);
double negative_min = std::numeric_limits<double>::lowest();
//backslash is to remove linebreaks here
std::cout << "Likely negative infinity: \n" << negative_min -
1000000000000000000000000000000000000000000000000000000000000\
0000000000000000000000000000000000000000000000000000000000000\
0000000000000000000000000000000000000000000000000000000000000\
0000000000000000000000000000000000000000000000000000000000000\
0000000000000000000000000000000000000000000000000.0 << '\n';
std::cout << negative_min + negative_min << '\n';
double positive_min = std::numeric_limits<double>::min();
std::cout << negative_min / positive_min << '\n';
}-0.0
Meglepő lehet, hogy a lebegőpontos számok esetén negatív nulla érték is létezik. Pedig ennek a létjogosultsága hasonló a végtelenéhez. Ha egy nullához közeli negatív számot megszorzunk egy nullához közeli pozitív számmal, vagy elosztunk egy nagyon nagy pozitív számmal, akkor olyan kicsi számot kapunk, ami már nem ábrázolható például a double típus keretein belül, hiszen egy double típusú érték tárolásához is véges mennyiségű memória áll rendelkezésre. Ha egy lebegőpontos számítás eredménye -0, mégiscsak tudunk tippelni arra, hogy nullához közeli negatív számmal dolgoztunk.
//negative zero test
#include <iostream>
#include <limits>
int main() {
double positive_min = std::numeric_limits<double>::min();
double positive_max = std::numeric_limits<double>::max();
std::cout << positive_min << '\n';
std::cout << positive_min * positive_min << '\n';
std::cout << -1 * positive_min * positive_min << '\n';
std::cout << -1 * positive_min / positive_max << '\n';
}Bár a lebegőpontos típusok esetén az egyenlőségvizsgálat sokszor megbízhatatlan, a negatív nulla egyenlő kell hogy legyen a nullával.
#include <iostream>
int main(){
std::cout.setf(std::ios::boolalpha);
std::cout << "negative zero equals to zero?\n" << (-0.0 == 0.0) << '\n';
}nan
A lebegőpntos típusok esetén a nan értékkel is találkozhatunk, ami a not a number (nem szám) rövidítése, mely jellemzően a matematikában nem értelmezhető műveletek eredményeként jöhet ki, mint például ha a végtelent elosztjuk végtelennel.
//nan test
#include <iostream>
#include <limits>
int main() {
double inf_example = std::numeric_limits<double>::infinity();
std::cout << 0.0/0 << '\n';
std::cout << inf_example * 0.0 << '\n';
std::cout << inf_example - inf_example << '\n';
std::cout << inf_example / inf_example << '\n';
}Ha esetleg a nan értéket szeretnénk adni egy lebegőpontos típusú változónak, akkor a C++ standard library limits headerjének includeolása esetén a std::numeric_limits<double>::quiet_NaN() kifejezést használhatjuk, vagy esetleg a C nyelvből átvett NAN kifejezéssel is találkozhatunk (amihez a cmath headert kell includeolni).
//nan as value
#include <iostream>
#include <limits>
int main() {
double nan_example = std::numeric_limits<double>::quiet_NaN();
std::cout << nan_example << '\n';
}Fontos tudni, hogy a nan nem egyenlő saját magával (nem is kisebb és nem is nagyobb), ami persze logikus, hiszen miért is tekintenénk egyenértékűnek mondjuk a végtelen osztva végtelennel és a nulla osztva nullával kifejezéseket, viszont ez azt jelenti, hogy ha meg akarjuk vizsgálni, hogy egy változó értéke nan-e vagy sem, akkor nem használhatunk egyenlőségvizsgálatot (ez ugyebár a dupla egyenlőségjel operátor, amiről későbbi tananyagrészben lesz szó), hanem erre a célra például a C++ standard library cmath header fájljában lévő isnan függvényt használhatjuk.
//isnan
#include <iostream>
#include <cmath>
int main() {
std::cout.setf(std::ios::boolalpha);
double example = 0.0/0;
std::cout << "example variable's value is nan?\n";
std::cout << std::isnan(example) << '\n';
}//error
#include <limits>
#include <cmath>
//...
std::cout << (example == std::numeric_limits<double>::quiet_NaN()) << '\n';
std::cout << (example == NAN) << '\n';
//...A C++ nyelvben a nan nem lehet szöveg számmá történő konvertálásának eredménye, mint például Javascriptben.
Egyéb tananyagok a lebegőpontos típusokról:
Egyéb tudnivalók
currency type
Egyes programozási nyelvekben (pl. basic) találkozhatunk a currency (pénznem) típussal is, amivel jellemzően 2-4 tizedesjegy pontossággal tárolhatunk számokat. A háttérben azonban az ilyen típusú értékek egész számként vannak tárolva, a tizedes vessző helye pedig rögzített. Mint ahogy a nevéből sejthető, például pénzügyi számításokhoz használják, ahol nem megengedhetőek a lebegőpontos típusok ábrázolásából eredő kerekítési hibák.
- docs.microsoft.com - vba currency data type
- openoffice wiki, basic guide - numbers
- stackoverflow.com - best way to store currency values in c++
típusok matematikai háttere
Jellemzően felsőfokú tanulmányok során elképzelhető, hogy azt is meg kell tanulni, hogy az int típusokban vagy a lebegőpontos típusokban pontosan hogyan vannak tárolva az értékek. Ebben a tananyagban erre nem térek ki, de további tananyagokat tudok ajánlani:
- C++ Weekly - Two's Complement Binary Math (videó)
- Porkoláb Zoltán (ELTE) - lebegőpontos számok
- John Farrier - Demystifying Floating Point (videó)
Hogyan számítható ki egy int típus méretéből a legnagyobb, legkisebb értéke?
A mai átlagos felhasználói számítógépeken például az int típus lehetséges legkisebb értéke -2147483648, a legnagyobb értéke pedig 2147483647.
Szintén a mai átlagos felhasználói számítógépeken az int típus 4 bájtos, azaz 32 bites (1 bájt = 8 bit, 8*4=32). A számítógép a számokat 2-es számrendszerben tárolja, vagyis egy számjegy vagy 0, vagy 1 lehet. 32 biten 32 számjegy tárolható (a bit jelentése binary digit, azaz 2-es számrendszerbeli számjegy). Ha 32-szer kell kiválasztani vagy 0-t vagy 1-et, az a kombinatorikában ismétléses variáció, aminek a képlete (a 32 és a 0 és 1 esetén, ami kétféle számjegy): 232.
232 = 4294967296
Az unsigned int lehetséges legnagyobb értéke 4294967295, mivel a legkisebb érték nem 1, hanem 0.
Az int típusban negatív számok is tárolhatóak, ezért a 4294967296 értéket el kell felezni, ami 2147483648, viszont mivel a 0 is szerepel az értékek között, ezért a legkisebb negatív szám -2147483648, a legnagyobb pozitív szám pedig 2147483647.
Előző tananyagrész: gyakori műveletek
Következő tananyagrész: alapvető típuskonverziók

